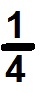Proyecto de aula:
Conociendo los números, a través de las compras
Objetivo del proyecto:
- Identificar e interpretar la información que proporcionan los números presentes en el entorno y utilizar números para comunicar información en forma oral y escrita, en situaciones correspondientes a distintos usos.
Nivel: 1° básico
Fundamentación:
Estimular a los niños para que puedan comprender el concepto de número a través de las diversas nociones básicas y lógicas matemáticas, tales como la noción de conjunto, noción de cantidad, noción de comparación, noción de clasificación, noción de seriación, noción de número.
A través de la adquisición de este conocimiento el niño podrá enfrentar los diversos problemas matemáticos que se le presenten en su vida cotidiana.
Actividades para realizar el proyecto:
1) Cuentan un objeto distribuidos al azar, pudiendo tomarlos y colocarlos a un lado, a medida que los cuentan.
- Se trabaja la noción de correspondencia, ya que podrán darse cuente que tiene mas elemento que otro compañero, o menos elementos que el otro compañero.
2) Cuentan varios conjuntos y comentan acerca de la utilidad de la información obtenida:
- Se trabaja la noción de conjunto, ya que los alumnos observan varios conjuntos y pueden comparar uno con otro, observando sus semejanzas y diferencias
- Cuentan sus pertenencias tales como lápices, láminas de un álbum, bolitas, y comentan para que les podrían servir saber cuántos son.
- Se encuentra presente la noción de cantidad, ya que comparan conjuntos utilizando algunos cuantificador [todos, algunos, ninguno, más que–menos que, tantos como]
- Dicen la secuencia del 6 al 9 y la comparan con la secuencia 16 al 19 y del 26 al 29 en lo que respecta a los nombres de los números. Guiados por el docente, sacan conclusiones en cuanto a sus diferencias y semejanzas. Para facilitar esta tarea, el docente puede anotar en la pizarra los números dichos por los estudiantes. Considerando las conclusiones a que han llegado, conversan acerca de qué otro nombre podría tener el once, doce, trece, catorce y quince.
- Guiados por el docente, conversan acerca de qué sucede después de un número terminado en nueve. Por ejemplo, después del “nueve”, del “diecinueve” del “veintinueve”.
3) El profesor pide a un alumno que comience la secuencia a partir de un número dado. En cualquier momento señala a otro alumno (a), quien debe continuar diciendo la secuencia ya sea de forma ascendente o descendente según lo destaque a partir de un gesto (pulgar hacia arriba o hacia abajo) o palabra concertada previamente (más o menos). Se continúa con la actividad hasta que haya participado todo el curso.
- Se trabaja la noción de seriación: porque se tiene que seguir un cierto orden o secuencia determinada, ya que deberán seguir una secuencia a partir del número dado
- Se comunica a los alumnos que la próxima semana se realizará una visita a un supermercado, preguntándoles si en alguna ocasión han visitado uno realizando una lluvia de idea con referencia a su experiencia.
4) Con la visita al supermercado, donde los alumnos observarán y registrarán en una bitácora como se compone este, tanto en la cantidad de pasillos y que se encuentra en aquel, las cantidades de cajas de pago, los guardias.
- Se utiliza la noción básica de espacio, porque podrán descubrir a través de su experiencia vivida el espacio físico que utiliza cada elemento observado por ellos.
- Los alumnos identificaran en su bitácora en que número de pasillo se encuentra cada alimentos, tal como frutas, artículos escolares, lácteos, fideos.
- Se trabaja la noción de clasificación, ya que al registrar en las bitácoras los niños pueden descubrir las diferencias y similitudes de los objetos y así poder clasificarlos en algún conjunto y subconjunto
- En la ubicación, de las frutas, los alumnos deberán identificar y anotar en su bitácora, cuantas clases de frutas se encuentran, y contar cuantos tipos de frutas hay.
- Noción de seriación: los alumnos deben ver que se sigue un orden o secuencia determinada.
- Noción de clasificación: se dan cuenta que las frutas se encuentran agrupadas según el tipo que sea y el color que tengan [en el caso de la manzana]
- En la ubicación de los artículos escolares, los alumnos deberán identificar y anotar en su bitácora, que artículos escolares se encuentran.
- Noción de seriación: se ve que cada artículo escolar tiene su orden o una secuencia determinada. Noción de clasificación: cada articulo escolar está separado.
- En la ubicación de los lácteos, los alumnos deberán identificar y anotar en su bitácora, las clases de lácteos que hay (leches según el sabor, si es en caja o botella, yogurth si es con cereal, trocitos de fruta o solo) y contar cuantos tipos de lácteos hay.
- Noción de seriación: se ve que cada lácteo tiene su orden o una secuencia determinada. Noción de clasificación: cada lácteo está separada según la clase de lácteo que hay
- En la ubicación de los fideos, los alumnos deberán identificar y anotar en su bitácora, cuantas clases de fideos se encuentran, y contar cuantos tipos de fideos hay.
- Noción de seriación: se ve que cada fideos tiene su orden o una secuencia determinada. Noción de clasificación: cada fideo está separada según la clase de fideos que hay.
- La docente les comunica que a través de los registros de sus bitácoras, deberán realizar una construcción de un mini-supermercado y para eso la próxima clase deben traer materiales para comenzar la construcción del mini-supermercado, los cuales pueden ser, cartones, pegamento, tijeras, plumones, lápices de colores, recortes, etc.
5) Cada alumno comenta sobre la experiencia que tuvieron con la visita al supermercado, dando a conocer las observaciones registradas en sus bitácoras.
- Se les informa que la realización del mini-supermercado será hecho en un periodo de 7 clases aproximadamente, comenzando con el pasillo de los fideos donde cada alumno deberá traer distintos tipos de fruta para que el pasillo quede bien abastecido.
- Posterior a la visita al supermercado en conjunto se realizará un mini supermercado, en el cual los alumnos diseñarán (publicidad, etiquetas de precio para los productos y dinero diseñado por ellos) clasificando los alimentos y ubicándolo en el pasillo correspondiente a cada producto.
- El mismo procedimiento tendrá la siguiente clase, pero esta vez con los lácteos (leches según el sabor, si es en caja o botella, yogurth si es con cereal, trocitos de fruta o solo), posteriormente con los frutas (manzanas [roja/verde], naranjas, plátano, pera), y finalizando con los artículos escolares (cuadernos, lápices de colores, gomas de borrar, reglas, sacapuntas, tijeras)
- Se comunica a los alumnos que la próxima clase deberán traer distintos tipos de fideos (corbatas, espirales, canutones, de preferencia) para abrir el mini-supermercado. El primer día será el día del fideo.
6) Luego de la visita al supermercado y ya diseñado el mini-supermercado por los alumnos, cada uno traerá fideos de distintos tipos, el cual serán clasificadas por ellos mismo diseñando las bolsas.
- Una vez ya clasificadas los fideos, procederán a contar la cantidad de bolsas de fideos (las bolsitas serán diseñadas y fabricadas por ellos mismos).
- Los alumnos como curso decidirán el valor que le darán a cada tipo de fideo (diseñando ellos mismos las etiquetas de precios)
- La actividad consiste en que se realizará juegos de roles, donde la mitad del curso tomara el rol de vendedores, cajeros, promotores del mini-supermercado, mientras la otra mitad tendrá el rol de cliente y deberán comprar los productos que se están vendiendo en esta oportunidad. Al cabo de 15 a 20 minutos los roles se invertirán.
- Al culminar la actividad anterior la docente procederá a cerrar la clase preguntándole a los niños que diferencia existe entre los producto que se vendieron (textura, tamaño, consistencia, colores, etc.)
- La profesora comunica que la próxima clase deben traer distintos tipos de lácteos (leches según el sabor, si es en caja o botella, yogurth si es con cereal, trocitos de fruta o solo) Será el día del lácteo.
7) Posteriormente los alumnos traerá lácteos de distintos tipos, el cual serán clasificadas por ellos mismo.
- Una vez ya clasificadas los lácteos, procederán a contar la cantidad de cada tipo de lácteos traídos
- Los alumnos como curso decidirán el valor que le darán a cada tipo de lácteo (diseñando ellos mismos las etiquetas de precios)
- La actividad consiste en que se realizará juegos de roles, donde la mitad del curso tomara el rol de vendedores, cajeros, promotores del mini-supermercado, mientras la otra mitad tendrá el rol de cliente y deberán comprar los productos que se están vendiendo en esta oportunidad. Al cabo de 15 a 20 minutos los roles se invertirán.
- Al culminar la actividad anterior la docente procederá a cerrar la clase preguntándole a los niños que diferencia existe entre los producto que se vendieron (sabor, tipo de yogurth, etc.)
- La profesora les comunica a los alumnos que la próxima semana deben trae frutas (manzanas[verdes/rojas], naranjas, plátanos, peras) para realizar el día de la fruta.
8) Los alumnos traerán frutas de distintos tipos, el cual serán clasificadas por ellos mismo.
- Una vez ya clasificadas las frutas, procederán a contar la cantidad, cuantos tipos de frutas hay y colocarlas en su respectiva ubicación en el mini-supermercado.
- Los alumnos como curso decidirán el valor que le darán a cada tipo de fruta (diseñando ellos mismas las etiquetas de precios)
- La actividad consiste en que se realizará juegos de roles, donde la mitad del curso tomara el rol de vendedores, cajeros, promotores del mini-supermercado, mientras la otra mitad tendrá el rol de cliente y deberán comprar los productos que se están vendiendo en esta oportunidad. Al cabo de 15 a 20 minutos los roles se invertirán.
- Al culminar la actividad anterior la docente procederá a cerrar la clase preguntándole a los niños que diferencia existe entre los producto que se vendieron (tamaño, textura, color, etc.)
- Al culminar esta actividad se les comunicara a los alumnos que la próxima semana realizaran el día de los útiles escolares, donde utilizaran sus propios lápices, cuadernos, reglas, tijeras, etc. Será el día de los útiles escolares.
9) Para finalizar los alumnos traerán útiles escolares(los utilizados en la sala de clases) de distintos tipos, el cual serán clasificadas por ellos mismo.
- Una vez ya clasificadas los útiles escolares procederán a contar la cantidad de útiles escolares que hay.
- Los alumnos como curso decidirán el valor que le darán a cada tipo de útiles escolares (diseñando ellos mismas las etiquetas de precios)
- La actividad consiste en que se realizará juegos de roles, donde la mitad del curso tomara el rol de vendedores, cajeros, promotores del mini-supermercado, mientras la otra mitad tendrá el rol de cliente y deberán comprar los productos que se están vendiendo en esta oportunidad. Al cabo de 15 a 20 minutos los roles se invertirán.
- Al culminar la actividad anterior la docente procederá a cerrar la clase preguntándole a los niños que diferencia existe entre los producto que se vendieron (tamaño, textura, color, etc.)
- En la actividad 6, 7, 8, 9 los alumnos desarrollan la noción de clasificación: porque tienen que ser capaz de ir clasificando los elementos según su forma diferencia, etc. También se desarrolla la noción de seriación: ya que tienen que ser capaz de ir ordenando los elementos en una forma lógica.
10) Para cerrar la actividad del mini-supermercado, se procederá hacer una retroalimentación sobre las actividades realizadas, donde los niños podrán compartir sus experiencias, comentar que aprendieron, que les costó más realizar,.
Estrategia didáctica:
Se trabajara en forma grupal e individual según la actividad que se realice.
Recursos a utilizar:
Material concreto, cartulinas, hojas blancas (para hacer el dinero que se utilizará para comprar en el mini-supermercado), lápices de colores, cuadernos, guías.
Tiempo del proyecto:
Mensual
Evaluación:
Evaluaciones clase a clase y semanal (a través de los registros de las bitácoras), para controlar el proceso de aprendizaje.
Evaluaciones sumativas.
Creado por: Nayadeth Aravena - Mónica Urra
